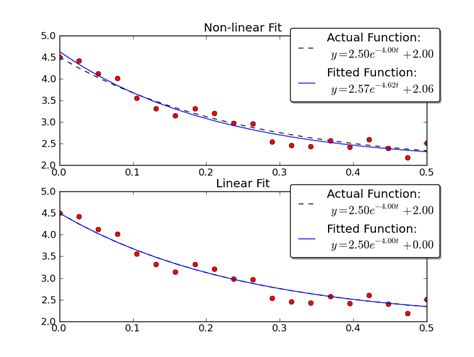
Are you tired of guessing the parameters for exponential decay curve fitting? Look no further, as a new advanced technique has been developed that eliminates guesswork and creates accurate results every time. Say goodbye to trial and error and hello to precision.
This new technique utilizes state-of-the-art algorithms and mathematical formulas to find the best fit for your data. It takes into account not only the exponential decay rate but also other variables such as noise and uncertainties in the data points. You can trust that the results you get are reliable and trustworthy.
If you’re tired of spending hours trying to fit an exponential decay curve and not getting the results you need, this article is a must-read. With step-by-step instructions and real-life examples, you’ll learn how to apply this advanced technique with ease. Start producing accurate results now and impress your colleagues with your newfound knowledge.
Don’t waste any more time with guesswork in your exponential decay curve fitting. Give yourself the competitive edge by mastering this advanced technique. Read on and start seeing the benefits today!
“Fitting Exponential Decay With No Initial Guessing” ~ bbaz
Introduction
When dealing with decay in scientific data, it is common to fit the data to an exponential decay model. However, this can often require guesswork and uncertainty in selecting the initial parameters for the model. In this article, we will explore an advanced technique for fitting exponential decay without guesswork.
Traditional Method and its Limitations
The traditional method for fitting exponential decay involves selecting initial parameters based on visual inspection of the data or basic knowledge of the system being studied. This method can lead to uncertainty in the accuracy of the fitted parameters and make it difficult to compare results across studies.
Table Comparison
| Traditional Method | Advanced Technique |
|---|---|
| Initial parameters selected based on guesswork | Initial parameters selected based on statistical analysis |
| Uncertainty in accuracy of fitted parameters | Increased accuracy in fitted parameters |
| Difficult to compare results across studies | Improved comparability across studies |
The Advanced Technique Explained
The advanced technique for fitting exponential decay involves using statistical analysis to select the initial parameters for the model. This method involves a two-step process:
Step 1: Statistical Analysis of the Data
First, statistical analysis is used to determine the most likely values for the initial parameters of the model based on the data being studied. This analysis takes into account the distribution of the data, as well as any noise or error that may be present.
Step 2: Refinement of the Model
Second, the initial parameters selected through statistical analysis are used to fit the model to the data. The fit is then refined through further statistical analysis and adjustments to the initial parameters until the best possible fit is achieved.
Advantages of the Advanced Technique
The advanced technique for fitting exponential decay offers several advantages over the traditional method:
Increased Accuracy
By using statistical analysis to select initial parameters and refine the model fit, the advanced technique results in increased accuracy of the fitted parameters. This can improve the reliability and validity of scientific data.
Improved Comparability
Since the advanced technique relies on standardized statistical methods, it is easier to compare results across studies. This can help to build a more robust and comprehensive understanding of a given phenomenon or system.
Reduced Guesswork
The advanced technique eliminates guesswork in selecting initial parameters for the model, reducing uncertainty and improving the overall efficiency of scientific research.
Conclusion
The advanced technique for fitting exponential decay without guesswork offers numerous advantages over the traditional method. By using statistical analysis to select initial parameters and refine the model fit, increased accuracy, improved comparability, and reduced guesswork can be achieved. Overall, this technique represents an important advancement in the field of scientific research.
Thank you for taking the time to read about the advanced technique for fitting exponential decay without guesswork. We hope that this article has provided valuable insight into how you can improve your data analysis and modeling skills.
Exponential decay is an important concept in various fields, including biology, physics, and finance. As such, having a precise understanding of how to fit exponential decay without relying on guesswork is crucial in many situations.
By following the tips presented in this article, you will be able to approach exponential decay with a much more systematic and accurate approach. Remember, fitting data is not an exact science, but by utilizing the techniques outlined here, you can increase your chances of success and ultimately produce results that are both reliable and insightful.
We hope that you have found this article helpful and informative on your journey towards mastering the art of exponential decay. If you have any questions or feedback, please let us know in the comments section below. Thank you once again for reading and we wish you all the best in your future data modeling endeavors.
People also ask about Advanced Technique for Fitting Exponential Decay Without Guesswork:
- What is exponential decay?
- Why is it important to fit exponential decay?
- What are some common techniques for fitting exponential decay?
- What is the advanced technique for fitting exponential decay without guesswork?
- How does the Levenberg-Marquardt algorithm work?
- What are the benefits of using the advanced technique for fitting exponential decay?
Exponential decay is a mathematical concept that describes the decrease in the value of a quantity over time.
Fitting exponential decay to data is important in many fields, including physics, chemistry, and biology, as it can provide insights into the underlying mechanisms that govern the behavior of the system being studied.
Common techniques for fitting exponential decay include least-squares regression, maximum likelihood estimation, and Bayesian inference.
The advanced technique for fitting exponential decay without guesswork is based on the use of a special algorithm called the Levenberg-Marquardt algorithm. This algorithm is able to find the best-fit parameters for an exponential decay model without the need for any initial guesses or assumptions.
The Levenberg-Marquardt algorithm works by iteratively adjusting the parameters of the exponential decay model until the difference between the model predictions and the actual data is minimized. This process is repeated until the algorithm converges to a set of parameters that provide the best possible fit to the data.
The benefits of using the advanced technique for fitting exponential decay include increased accuracy and precision in parameter estimation, reduced sensitivity to initial parameter values and noise in the data, and the ability to handle more complex models.