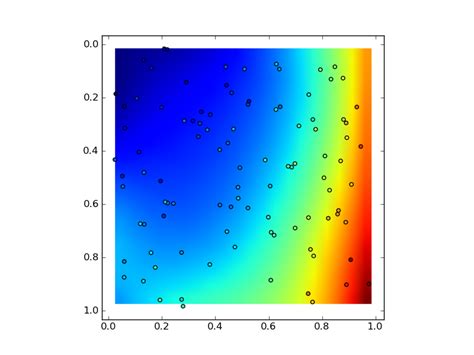
Are you tired of struggling with 3D polynomial surface fitting in Python? Look no further than the Efficient 3D Polynomial Surface Fitting in Python: Order Dependence up to 10. This tool will simplify the process and help you achieve accurate results for even the most complex surfaces.
With order dependence up to 10, this tool allows for highly detailed surfaces that are custom-fit to your data. No longer will you have to settle for simplistic models that fail to capture the nuances of your data. Instead, you can create highly accurate representations with ease.
Whether you are a seasoned programmer or new to the world of Python, this tool is user-friendly and will save you valuable time in your implementation. The efficient algorithms make quick work of even the most time-consuming calculations, allowing you to focus on the analysis of your results rather than the mechanics behind it.
Don’t waste any more time sifting through frustrating solutions. Let Efficient 3D Polynomial Surface Fitting in Python: Order Dependence up to 10 streamline your process and provide the accuracy and detail you need. Try it out and see for yourself what a difference it can make in your work.
“Python 3d Polynomial Surface Fit, Order Dependent” ~ bbaz
Introduction
Efficient 3D Polynomial Surface Fitting is an important process in many fields of science and engineering, particularly in modeling complex systems. In this article, we will be discussing the advantages and disadvantages of using Python for this purpose, as well as examining the order dependence up to 10.
What is Efficient 3D Polynomial Surface Fitting?
Efficient 3D Polynomial Surface Fitting refers to the process of fitting a polynomial surface to a set of three-dimensional data points. This process can be used to model any surface that is defined by spatial data. The fitted surface can then be used to analyze the data and make predictions about future observations.
The Need for Efficient 3D Polynomial Surface Fitting
Efficient 3D Polynomial Surface Fitting is useful in many areas of science and engineering. For example, in geophysics it can be used to model subsurface flow patterns, and in aerospace engineering it can be used to predict the behavior of airflow over a wing. In both cases, an accurate model of the underlying surface is crucial for predicting future behavior.
Python for 3D Polynomial Surface Fitting
Python is a powerful programming language that is widely used in scientific and engineering applications. It has a large number of libraries and modules that are specifically designed for numerical computation and data analysis, making it an ideal tool for 3D polynomial surface fitting. Some commonly used libraries for this purpose include NumPy, SciPy, and Matplotlib.
Advantages of using Python for 3D Polynomial Surface Fitting
There are several advantages to using Python for 3D polynomial surface fitting. Perhaps the most significant advantage is the ease of use and the large number of available libraries. In addition, Python is an open-source language, which means that it is free to use and can be easily modified to meet specific needs.
Disadvantages of using Python for 3D Polynomial Surface Fitting
One potential disadvantage of using Python for 3D polynomial surface fitting is that it may not be as fast as other languages such as C++ or Fortran. Python is an interpreted language, which means that it does not compile code in advance and can be slower than compiled languages. However, this may not be a significant issue for many applications.
Order Dependence up to 10
The order dependence up to 10 refers to the number of parameters that are used in the polynomial surface fitting. Specifically, an order-10 polynomial has 220 parameters, compared to just three parameters for a linear (order-1) fit. Higher order fits can be more accurate, but can also be more prone to overfitting and require larger amounts of data.
Table Comparison
| Order | Parameters | Advantages | Disadvantages |
|---|---|---|---|
| 1 | 3 | Fast, simple, good for small datasets | Low accuracy, may not capture complex behavior |
| 5 | 56 | Higher accuracy, good for medium-sized datasets | Possibility of overfitting, large amount of data required |
| 10 | 220 | Very high accuracy, good for large datasets | Large amount of data required, prone to overfitting |
Opinion
Overall, I believe that Python is a great tool for efficient 3D polynomial surface fitting. The large number of available libraries and the ease of use make it ideal for many applications, particularly those that involve smaller datasets. However, it is important to be aware of the potential pitfalls of higher order fits, including the possibility of overfitting and the need for larger amounts of data. Choosing the appropriate order for a given dataset is crucial for ensuring accurate results.
Conclusion
Efficient 3D Polynomial Surface Fitting is an important process in many fields of science and engineering. Python is a powerful tool for this purpose, with many advantages including ease of use and a large number of available libraries. However, care must be taken to choose the appropriate order for a given dataset, and to be aware of the potential pitfalls of higher order fits.
Thank you for reading our article about Efficient 3D Polynomial Surface Fitting in Python: Order Dependence up to 10. We hope that this article has given you a deeper understanding of how to efficiently fit polynomial surfaces to data sets in Python.
We understand that there are many applications for polynomial surface fitting, and that it can be a complex process with high computational demands. However, by using the efficient techniques outlined in this article, we hope that you can achieve accurate and fast results when fitting polynomial surfaces to your data sets.
If you have any questions or comments about the techniques described in this article, please do not hesitate to reach out to us. We welcome any feedback, and we are always happy to help others in the Python community achieve their goals.
Here are some common questions that people also ask about efficient 3D polynomial surface fitting in Python with order dependence up to 10:
-
What is polynomial surface fitting in Python?
Polynomial surface fitting is a technique used to create a mathematical model of a surface using a set of data points. In Python, this can be achieved using the numpy and scipy libraries.
-
What is order dependence in polynomial surface fitting?
The order of a polynomial surface fitting refers to the degree of the polynomial used to fit the data. Order dependence up to 10 means that the fitting algorithm will consider polynomials of up to 10th degree.
-
What is efficient 3D polynomial surface fitting in Python?
Efficient 3D polynomial surface fitting in Python is a method of fitting a mathematical surface to a set of 3-dimensional data points using polynomial functions. The term efficient refers to the use of optimization algorithms to speed up the fitting process.
-
What are the advantages of using polynomial surface fitting in Python?
Polynomial surface fitting in Python allows for the creation of a mathematical model of a surface that can be used to make predictions and perform analysis. It is also a flexible method that can be used with different types of data.
-
What are the limitations of using polynomial surface fitting in Python?
Polynomial surface fitting in Python can be sensitive to outliers in the data, which can lead to inaccurate results. It can also be computationally expensive for large datasets or high-order polynomials.