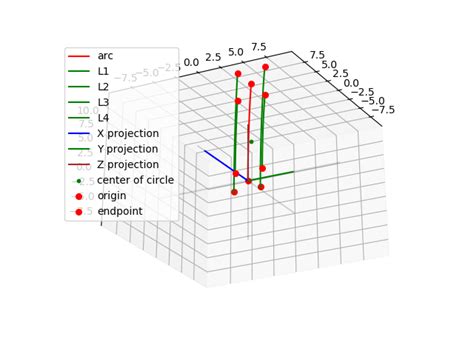
Do you find the task of connecting scatter points in 3D space time-consuming and tedious? Look no further, as we provide you with a guide on how to do it efficiently. Say goodbye to manual point by point connections and embrace a faster, more automated approach.
With our tips, you will learn how to make use of programming languages such as Python and MATLAB, as well as specialized software like CloudCompare and MeshLab, to create meshes and connect the points in record time. Additionally, we will teach you how to use statistical methods such as Delaunay triangulation and Voronoi tessellation to simplify the process of joining the scattered points into a coherent surface.
If you are someone who works in fields such as 3D modeling, mechanical engineering, or geology, then this guide is for you. We understand the importance of time and accuracy in your work, and our aim is to help you achieve both with ease. By the end of this article, you will have the necessary tools and knowledge to efficiently connect scatter points and create stunning 3D models, maps, and designs.
So, what are you waiting for? Dive into our guide and start exploring the world of efficient scatter point connection in 3D space. Trust us, it will revolutionize the way you work and save you countless hours of frustration.
“How Can I Connect Scatter Points In A 3d Space?” ~ bbaz
Introduction
Efficiently Connect Scatter Points in 3D Space is a crucial operation in many fields that utilize 3D data. It is essential to connect the scatter points efficiently to realize the full potential of the data. This blog post will provide a guide on how to efficiently connect scatter points in 3D space.
The Challenge of Connecting Scatter Points
The challenge with connecting scatter points in 3D space is the complexity of the process. There are several algorithms that can be used for this process, and each algorithm has its unique advantages and disadvantages. It is essential to choose the correct algorithm that will provide the desired result while minimizing computational costs.
Algorithm Comparison
| Algorithm | Advantages | Disadvantages |
|---|---|---|
| Nearest Neighbor | Simple | Not suitable for complex shapes |
| Alpha Shape | Efficient for complex shapes | Requires tuning of alpha parameter |
| Convex Hull | Fast | Not suitable for non-convex shapes |
The Nearest Neighbor Algorithm
The nearest neighbor algorithm connects each point to its nearest neighbor based on the Euclidean distance. The algorithm is simple and efficient but is not suitable for complex shapes that require more sophisticated connections.
Pros
- Simple and easy to implement.
- Efficient for small data sets.
Cons
- Not suitable for complex shapes.
- Can result in noisy connections.
The Alpha Shape Algorithm
The alpha shape algorithm is suitable for complex shapes and involves two parameters, the alpha value, and the radius. The alpha value determines the shape of the object, while the radius determines the size. This algorithm produces a smooth and accurate connection of points.
Pros
- Suitable for complex shapes.
- Produces a smooth and accurate connection of points.
Cons
- Requires tuning of alpha parameter.
- May not work well for noisy data sets.
The Convex Hull Algorithm
The convex hull algorithm creates a polygon around the points, allowing for the connection of the points. The algorithm is efficient for large data sets and is fast. However, it is not suitable for non-convex shapes.
Pros
- Fast and efficient.
- Suitable for large data sets.
Cons
- Not suitable for non-convex shapes.
- May leave gaps in the connection of points.
Conclusion
The choice of algorithm for connecting scatter points in 3D space depends on the shape of the object, the size of the data set, and the desired precision. The three algorithms discussed in this blog post are the nearest neighbor algorithm, alpha shape algorithm, and the Convex Hull algorithm. The decision on which algorithm to use should be based on a careful analysis of the data set and the desired result.
Thank you for taking the time to read this guide on efficiently connecting scatter points in 3D space. We hope that the information provided here has given you a better understanding of the different methods and techniques available to you.
Remember that when working with scatter points in 3D space, organization and accuracy are key. Taking the time to properly label and group your data can save you countless hours down the line, and utilizing tools like Python and matplotlib can greatly streamline the process of creating visual representations of your data.
With these tips and tricks in mind, you should be well-equipped to tackle any scatter point project that comes your way. As always, never hesitate to reach out to the communities and resources available online for additional guidance and support.
People Also Ask about Efficiently Connect Scatter Points in 3D Space – A Guide:
- What is the best way to connect scatter points in 3D space?
- The best way to connect scatter points in 3D space is to use a curve fitting algorithm such as interpolation or regression analysis.
- Some common curve fitting algorithms used for connecting scatter points in 3D space include cubic splines, linear regression, and polynomial regression.
- You can visualize the connected scatter points in 3D space using a 3D scatter plot with the connected points represented by a line or curve.
- There are several software options available for efficiently connecting scatter points in 3D space, including MATLAB, Python, and R.
- You can ensure that the connected scatter points accurately represent the data by choosing an appropriate curve fitting algorithm and evaluating the goodness of fit metrics such as R-squared value and residual plots.