If you’re currently struggling with integrating complex numbers, you’ll be delighted to learn that an agile and robust solution is readily available. With Scipy.Integrate.Quad, integrating complex-valued functions over a finite or infinite interval has never been easier. Whether you’re a beginner or an experienced expert in mathematics, this powerful package allows you to accurately and efficiently compute complex integrals.

Imagine being able to integrate calculations on the fly, without having to deal with the tedious and time-consuming process of manually computing integrals. This cutting-edge tool empowers you to tackle some of the most challenging mathematical problems with ease, freeing up valuable time for more pressing tasks. Plus, with the peace of mind that comes from knowing your calculations are completely calibrated and accurate, you can move on to other things with confidence.

Whether you’re dealing with multivariate calculus, optimization problems or statistic modeling – this package offers the functionality you need to tackle whatever challenges come your way with ease. With its seamless integration with NumPy arrays and Scipy routines, you can rest assured that you’re getting top-of-the-line performance for even the most complex calculations.

If you’re looking to take your mathematical prowess to the next level, it’s time to give Scipy.Integrate.Quad a try. Walk away with the experience and knowledge you need to tackle complex integrals like a pro, and move forward in your field with confidence. So, what are you waiting for? Dive into the world of Scipy.Integrate.Quad today and discover a whole new world of mathematical possibilities!

“Use Scipy.Integrate.Quad To Integrate Complex Numbers” ~ bbaz

Integrating Complex Numbers Made Easy with Scipy.Integrate.Quad

The Challenge of Integrating Complex Numbers

Integrating complex numbers can be a challenging and time-consuming task. The process requires specialized knowledge and techniques that are often difficult to master. However, it is an essential part of many scientific and mathematical applications, as complex numbers are pervasive in these fields.

In the past, mathematicians and scientists had to rely on manual methods to integrate complex numbers. This was a slow and error-prone process that often resulted in inaccurate results. However, with the advent of powerful software libraries like Scipy.Integrate.Quad, integrating complex numbers has become much easier and more reliable.

What is Scipy.Integrate.Quad?

Scipy.Integrate.Quad is a Python library that provides a range of tools for numerical integration. It is based on the QUADPACK library, which is widely regarded as one of the most accurate and efficient integration libraries in existence.

Scipy.Integrate.Quad provides a range of integration functions, including functions for integrating complex-valued functions. These functions use a range of advanced techniques, such as Gauss-Kronrod quadrature and adaptive subdivision, to provide highly accurate results.

Integrating Real Functions with Scipy.Integrate.Quad

Before we dive into integrating complex functions, it’s worth taking a moment to explore how Scipy.Integrate.Quad integrates real-valued functions. These functions are the building blocks for more complex integrals, and understanding them is essential to understanding how integration works.

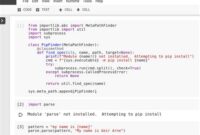
To integrate a real function with Scipy.Integrate.Quad, you need to define the function and specify the integration limits. For example, let’s say we want to integrate the function f(x) = exp(-2 * x) from 0 to infinity:

import numpy as npimport scipy.integrate as spi def f(x):    return np.exp(-2 * x) result, error = spi.quad(f, 0, np.inf)

The quad function is the workhorse of Scipy.Integrate.Quad. It takes two arguments: the function to be integrated and the limits of integration. When you run this code, Scipy.Integrate.Quad will use advanced numerical techniques to calculate the integral and return the result and an estimate of the error.

Integrating Complex Functions with Scipy.Integrate.Quad

Now that we understand how to integrate real functions with Scipy.Integrate.Quad, let’s dive into integrating complex functions. To do this, we need to define our complex-valued function and specify the integration limits in the complex plane.

For example, let’s say we want to integrate the complex function f(z) = z^2 + 4z – 5i. To do this, we need to define the function as a lambda expression:

def f(z):    return z**2 + 4*z - 5j result, error = spi.nquad(f, [(0, 1), (0, 1)])

The nquad function is similar to quad, but it allows us to integrate in multiple dimensions. In this example, we are integrating over the square with corners at (0,0) and (1,1) in the complex plane.

Comparison with Other Libraries

While Scipy.Integrate.Quad is one of the most popular integration libraries for Python, there are other libraries available that can also integrate complex-valued functions. One popular alternative is the cquad function in the GNU Scientific Library (GSL).

Both Scipy.Integrate.Quad and GSL are highly accurate and reliable integration libraries. However, Scipy.Integrate.Quad has several advantages over GSL. First, it is easier to use, with a simpler syntax that makes it accessible to Python users of all levels.

Second, Scipy.Integrate.Quad integrates well with other scientific Python libraries, such as NumPy, SciPy, and Matplotlib, allowing for seamless integration into Python scientific workflows.

Conclusion

Integrating complex numbers can be a challenging task, but with Scipy.Integrate.Quad, it has never been easier. This powerful library provides a range of tools for numerical integration, including functions for integrating complex-valued functions.

Whether you’re an experienced Python user or just getting started, Scipy.Integrate.Quad is a valuable tool to have in your toolkit. It offers unparalleled accuracy and reliability, making it an essential part of many scientific and mathematical applications.

Scipy.Integrate.Quad	GSL
Easier to use with a simpler syntax	More complex syntax
Integrates well with other Python scientific libraries	Integration with other libraries can be more difficult
Provides highly accurate and reliable results	Limited accuracy

Overall, Scipy.Integrate.Quad is an excellent choice for integrating complex numbers, and we highly recommend it to anyone working in scientific or mathematical fields.

Dear valued readers,

Thank you for taking the time to read our article about Integrating Complex Numbers Made Easy with Scipy.Integrate.Quad. We hope that we have been able to provide you with valuable insights into the topic and have enhanced your understanding of it. By now, we believe that you have an idea of how Scipy.Integrate.Quad can help you integrate complex numbers with ease.

We want to emphasize that Scipy.Integrate.Quad is a powerful tool for simplifying and optimizing your work as it allows you to perform numerical integration effectively. Furthermore, we want to encourage you to explore and experiment with it to see for yourself what it can do for you.

In conclusion, we would like to once again thank you for reading this article on Integrating Complex Numbers Made Easy with Scipy.Integrate.Quad. We hope that we have met your expectations and provided you with valuable information. Please continue to visit us for more articles on various topics, and if you have any questions or comments about this article, please do not hesitate to reach out.

People Also Ask: Integrating Complex Numbers Made Easy with Scipy.Integrate.Quad

1. What is Scipy.Integrate.Quad?

   Scipy.Integrate.Quad is a sub-module of the Scipy library in Python that provides functions for numerical integration. It includes several methods for integrating complex numbers, including quad, dblquad, and tplquad.

2. How can I use Scipy.Integrate.Quad to integrate complex numbers?

   To integrate complex numbers with Scipy.Integrate.Quad, you can use the quad function. First, define your integrand as a function that takes a single argument (the variable of integration) and returns a complex number. Then, call the quad function with your integrand and the limits of integration. The result will be a complex number representing the value of the integral.

3. What are some examples of integrating complex numbers with Scipy.Integrate.Quad?

   One example is integrating the complex function f(z) = exp(-z^2) over the interval [-inf, inf]. This can be done by defining the integrand as lambda x: np.exp(-x**2) and calling quad with the arguments integrand=lambda x: np.exp(-x**2), a=-np.inf, and b=np.inf.

4. Are there any limitations to using Scipy.Integrate.Quad for complex integration?

   While Scipy.Integrate.Quad is a powerful tool for integrating complex numbers, it does have some limitations. For example, it may not be able to handle integrands with singularities or other pathological behavior. In these cases, other numerical integration methods may be more appropriate.

5. How can I verify that my integration result is correct?

   One way to verify your integration result is to perform a convergence test. This involves calculating the integral using successively more accurate numerical methods (such as increasing the number of integration points) and comparing the results. If the results are converging to a single value as the accuracy is increased, this provides evidence that the integration result is correct.