Are you tired of struggling with finding the Greatest Common Divisor (GCD) of multiple numbers? Look no further than mastering the Euclidean Algorithm!
The Euclidean Algorithm is a classic method for finding the GCD of two numbers, but did you know it can also be applied to multiple numbers? By utilizing the power of recursion, you can efficiently find the GCD of any set of numbers.
So why waste time and effort manually calculating the GCD of multiple numbers? With the Euclidean Algorithm, you can easily and quickly solve any problem that comes your way. From academic assignments to real-life situations requiring mathematical analysis, mastering the Euclidean Algorithm will be a valuable tool in your arsenal.
Don’t miss out on the opportunity to enhance your mathematical skills and simplify your life. Read on to discover step-by-step instructions for applying the Euclidean Algorithm to multiple numbers, and start mastering GCD calculations today!
“Euclidean Algorithm (Gcd) With Multiple Numbers?” ~ bbaz
The Importance of GCD in Mathematics
In mathematics, the greatest common divisor (GCD) plays a significant role in solving problems involving prime factorization, modular arithmetic, and many other fields. It is defined as the largest positive integer that divides two or more numbers without a remainder. Finding the GCD for two numbers is relatively simple, but what if there are multiple numbers involved? This is where mastering GCD with multiple numbers becomes crucial.
Euclidean Algorithm: The Basics
Euclid’s algorithm is the most common method used to find the GCD of two numbers. It involves repeatedly dividing the larger number by the smaller number until the remainder is zero. The last non-zero remainder is then the GCD. This can be written mathematically as:

where a and b are the two numbers with a being greater or equal than b, and r, the remainder of b divided by a.
Extended Euclidean Algorithm: Solving for GCD with Multiple Numbers
However, when it comes to finding the GCD of multiple numbers using Euclid’s algorithm, additional steps must be taken. The extended Euclidean algorithm takes into account these extra steps, and it can also be used to solve for coefficients in Diophantine equations.
The Process of the Extended Euclidean Algorithm

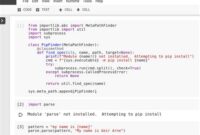
To use the extended Euclidian algorithm for multiple numbers, take the first two numbers in the list and find their GCD. Then, the GCD of the previous step and the next number in the list is found. This process is repeated until the end of the list, and the final GCD is found.
Comparison: GCD Algorithms
| GCD Algorithm | Pros | Cons |
|---|---|---|
| Euclidean Algorithm | Simple to understand and implement | Only applicable for finding GCD of two numbers |
| Extended Euclidean Algorithm | Can solve for GCD with multiple numbers | More complex to understand and implement |
Opinion: Which GCD Algorithm Should You Use?
There is no clear-cut answer to which algorithm is better to use since it depends on the situation. If you only need to find the GCD of two numbers, then Euclid’s algorithm is quick and straightforward. However, if there are multiple numbers involved, then the extended Euclidean algorithm might be the better option to use to save time and effort.
Real-Life Applications of GCD
GCD is used extensively in cryptography, telecommunications, and computer science. In cryptography, the GCD formula is used to determine whether two numbers are relatively prime, which is essential for creating secure encryption keys. In telecommunications, it plays a vital role in determining the rate and speed of digital transmissions.
Conclusion
Mastering GCD with multiple numbers using Euclidean algorithms is necessary for many different fields in mathematics, science, and technology. Both Euclidean and extended Euclidean algorithms have their pros and cons, but by knowing these differences, you can decide which one to use for your particular situation.
Thank you for taking the time to read our article on Mastering GCD with Multiple Numbers: Euclidean Algorithm Explained. We hope that you found it informative and helpful in understanding the process of finding the greatest common divisor of multiple numbers.
The Euclidean Algorithm is a simple and efficient method for finding the GCD of two or more numbers, and it can be applied to any set of integers. By following the steps outlined in this article, you can easily calculate the GCD of any set of numbers, no matter how large or complex they may be.
If you have any questions or comments about the Euclidean Algorithm or other mathematical concepts, please don’t hesitate to reach out to us. We are always happy to hear from our readers and to provide support and guidance as needed. Thank you again for visiting our blog, and we look forward to sharing more insights and information with you in the future.
People Also Ask about Mastering GCD with Multiple Numbers: Euclidean Algorithm Explained
- What is the Euclidean Algorithm?
- How do you use the Euclidean Algorithm to find the GCD of multiple numbers?
- Can the Euclidean Algorithm be used to find the LCM of multiple numbers?
- What is the significance of finding the GCD of multiple numbers?
- Is there any other method to find the GCD of multiple numbers?
The Euclidean Algorithm is a method for finding the greatest common divisor (GCD) of two or more numbers. It involves dividing the larger number by the smaller number and taking the remainder, then repeating the process with the smaller number and the remainder until the remainder is zero.
To find the GCD of multiple numbers using the Euclidean Algorithm, you can start by finding the GCD of the first two numbers. Then, you can use the result of this calculation and the next number in the list to find the GCD of three numbers, and so on. The final result will be the GCD of all of the numbers.
No, the Euclidean Algorithm is used to find the GCD of multiple numbers, not the LCM. To find the LCM, you can use the prime factorization method or the listing multiples method.
Finding the GCD of multiple numbers is useful in many areas of mathematics, including number theory, algebra, and cryptography. It can also be used in practical applications such as reducing fractions and simplifying complex calculations.
Yes, there are other methods to find the GCD of multiple numbers, such as the prime factorization method and the binary GCD algorithm. However, the Euclidean Algorithm is a simple and efficient method that can be used in most cases.