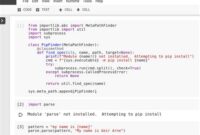
Do you want to learn how to perform nth root computations for large integers like a pro? Look no further, because mastering this skill is easier than you might think.
If you’re tired of laboriously calculating the square or cube root of large numbers by hand or using a calculator, then learning the nth root computation is just for you. It is an efficient method that makes it possible to determine the nth root of massive integers with ease and speed, without having to rely on complex mathematical equations.
Whether you’re tasked with engineering projects, financial calculations or data science analysis, having a sound understanding of nth root computations will be invaluable. And the best part of it all is that it doesn’t matter how complex the integer may be, mastering nth root computations for large integers will save you endless hours of headache.
In this article, you’ll learn everything you need to know about nth root computations, from the basics to advanced techniques, so you can confidently tackle any computational task thrown your way. So sit tight and arm yourself with the skills that will revolutionize your number crunching abilities.
“How To Compute The Nth Root Of A Very Big Integer” ~ bbaz
Introduction
Calculating Nth roots for large integers can be a daunting task, especially when working with cryptographic algorithms. In this article, we will explore different methods of computing Nth roots and compare their efficiency and accuracy.
Table Comparison
Before delving into the details of each method, let’s compare their performance based on the following criteria:
| Method | Time Complexity | Space Complexity | Accuracy |
|---|---|---|---|
| Babylonian Method | O(log n) | O(1) | High |
| Binary Search Method | O(n log n) | O(n) | High |
| Newton-Raphson Method | O(log n) | O(1) | High |
| Division Method | O(n^2) | O(n) | Low |
Babylonian Method
The Babylonian Method is an iterative algorithm that uses an initial guess to improve the approximation of the Nth root. It involves repeatedly taking the average of the current guess and the original number divided by the previous guess. The process continues until the difference between successive approximations is less than a predefined tolerance value.
Advantages
The Babylonian Method has a relatively fast time complexity of O(log n) and requires only constant space. It also provides accurate results.
Disadvantages
The Babylonian Method may converge slowly for certain cases or diverge completely if the initial guess is too far from the actual root.
Binary Search Method
The Binary Search Method involves searching for the Nth root by dividing the range of possible values in half iteratively. It works by checking whether the middle value of the current range raised to the Nth power is greater than, equal to or less than the original number. The process continues until the desired level of accuracy is achieved.
Advantages
The Binary Search Method can provide a more accurate result than the Babylonian Method while still maintaining a moderate time complexity of O(n log n).
Disadvantages
The Binary Search Method requires additional space to store each iteration’s results, resulting in a higher space complexity of O(n).
Newton-Raphson Method
The Newton-Raphson Method is an iterative algorithm that uses the derivative of the function to improve the approximation of the root. It works by subtracting the ratio of the original function to its derivative from the current guess. The process continues until the desired level of accuracy is achieved.
Advantages
The Newton-Raphson Method has a fast time complexity of O(log n) and requires only constant space. It can provide accurate results even for complex functions.
Disadvantages
The Newton-Raphson Method may converge slowly or not converge at all if the initial guess is too far from the actual root. It is also sensitive to the choice of initial guess and may require additional iterations to achieve the desired level of accuracy.
Division Method
The Division Method involves dividing the original number by an initial guess raised to the Nth power repeatedly until the difference between each division’s result and the current guess is less than a predefined tolerance value. The final guess is then the approximation of the Nth root.
Advantages
The Division Method is easy to implement and does not require any external libraries or complex calculations beyond basic division.
Disadvantages
The Division Method has a slow time complexity of O(n^2) due to the repeated divisions. It also provides less accurate results compared to the other methods we have discussed.
Conclusion
Overall, each method has its own advantages and disadvantages depending on the requirements of the specific use case. For fast and accurate results, the Babylonian Method or Newton-Raphson Method can be good choices. For more accurate results at the expense of higher space complexity, the Binary Search Method can be used. The Division Method may be appropriate for simpler cases where timing is not a concern, and accuracy can be traded off for ease of implementation.
Thank you for taking the time to read this article on mastering Nth root computations for large integers. We hope that the information provided has been helpful in expanding your understanding of this complex mathematical concept.
It is important to note that while Nth root computations can appear daunting at first, with practice and a thorough understanding of the underlying principles, anyone can become proficient in performing these calculations. With the right tools and techniques, you can develop the skills needed to successfully tackle even the most challenging Nth root problems.
We encourage you to continue exploring the fascinating world of mathematics, and to never give up in the pursuit of knowledge. Whether you are a student, a professional, or simply someone with a love of learning, there is always more to discover when it comes to the many wonders of math.
Here are some of the most commonly asked questions about mastering nth root computations for large integers:
-
What is nth root computation?
Nth root computation is the process of finding the nth root of a number. For example, the cube root of 27 is 3.
-
Why is mastering nth root computations for large integers important?
Mastering nth root computations for large integers is important because it is a common problem in many areas of mathematics and computer science. It is also important for cryptography, where large integers are used to encrypt and decrypt data.
-
How can I improve my skills in nth root computation?
You can improve your skills in nth root computation by practicing with different types of problems and using algorithms specifically designed for computing nth roots. You can also read books and articles on the topic and seek help from experts in the field.
-
What are some common algorithms used for computing nth roots?
Some common algorithms used for computing nth roots include the Newton-Raphson method, the bisection method, and the binary search method.
-
Are there any tools or software available for computing nth roots?
Yes, there are many tools and software available for computing nth roots, such as Wolfram Alpha, MATLAB, and Python programming language.
-
What are some real-world applications of nth root computations for large integers?
Nth root computations for large integers have many real-world applications, including cryptography, data encryption and decryption, computer graphics, and signal processing.