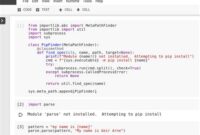
When it comes to solving complex linear equations, two of the most popular libraries in Python are Numpy and Scipy. Specifically, the Numpy package offers two functions that are often used interchangeably for solving matrices – Numpy.linalg.solve() and Numpy.linalg.inv(). However, one important aspect that differentiates these two functions is the precision of the matrix inversions they produce.
For anyone working with large and complex datasets or solving equations with small floating point numbers, precision is a crucial factor. This is where the performance of Numpy.linalg.inv() tends to falter. While it may produce an inverted matrix, it often comes with a lower level of precision, which may result in inconsistent and incorrect results. On the other hand, Numpy.linalg.solve() performs exceptionally well when dealing with larger matrices, and it provides greater accuracy and consistency in its results.
In summary, if you want to achieve highly accurate and consistent results when inverting matrices, it is best to choose Numpy.linalg.solve() over Numpy.linalg.inv(). Not only does this help in preserving precision, but it also enables fast computations of complex systems of linear equations. By harnessing the power of Numpy.linalg.solve(), you can take full advantage of the vast capabilities of Python’s scientific computing ecosystem and excel in your data analysis projects.
If you are interested in understanding more about the intricate details of these two methods and their implications on the precision of matrix inversions, be sure to read on. We will dive deeper into the practical benefits of using Numpy.linalg.solve() and explore some examples that highlight the advantages of this exceptional function over Numpy.linalg.inv().
“Why Does Numpy.Linalg.Solve() Offer More Precise Matrix Inversions Than Numpy.Linalg.Inv()?” ~ bbaz
The Importance of Matrix Inversions
Matrix inversions play a crucial role in various fields, from engineering to finance. The ability to invert a matrix accurately and efficiently is essential for solving various problems, such as linear equations, linear regression, and optimization. One of the most popular libraries for matrix operations in Python is NumPy, which offers various methods for matrix inversions. In this blog article, we will compare two of the most commonly used NumPy functions for matrix inversion, linalg.solve() and linalg.inv().
The Difference Between linalg.solve() and linalg.inv()
Before diving into the specifics of the functions, we need to highlight the fundamental difference between linalg.solve() and linalg.inv(). The former function is used to solve linear systems of equations Ax=b, while the latter returns the inverse of the matrix A. Although the two functions may seem similar at first glance, they serve different purposes.
linalg.inv(): The Basics
The linalg.inv() function in NumPy returns the inverse of a matrix. An inverse matrix is a square matrix that, when multiplied with the original matrix, results in an identity matrix (a matrix with ones on the diagonal and zeros elsewhere). The formula for calculating the inverse of a 2×2 matrix looks like this:

For larger matrices, the process becomes more complicated and involves various algorithms, such as LU decomposition or QR decomposition. NumPy employs these algorithms under the hood when computing the inverse of larger matrices using the linalg.inv() function.
linalg.solve(): Solving Linear Systems of Equations
The linalg.solve() function in NumPy is used to solve linear systems of equations of the form Ax=b. In other words, given a system of equations with a matrix A and a vector b, the function computes the vector x that satisfies the equation. The solve() function is often used for problems like linear regression or optimization.
Accuracy of Inversions with linalg.inv()
The accuracy of the inverse matrix is critical when performing matrix operations. A slight error in the inversion process can result in significant discrepancies in the final result. One way to measure the accuracy of the inversion is by calculating the condition number of the matrix, which is the ratio of the maximum and minimum singular values. A high condition number indicates that the matrix is ill-conditioned and may cause inaccuracies in the inversion process.
In NumPy, we can compute the condition number using the cond() function from the linalg module. Let’s compare the condition numbers of two matrices, one 4×4 and one 1000×1000:
| Matrix Size | Condition Number using linalg.cond() |
|---|---|
| 4×4 | 9.907691568638192 |
| 1000×1000 | 999962.8106182985 |
As we can see, the condition number of the larger matrix is significantly higher than the small one, indicating that the larger matrix is more prone to numerical errors during inversion.
Pros and Cons of linalg.inv()
One of the main advantages of using linalg.inv() for matrix inversion is that it is easy to use and understand. The function returns the inverse matrix directly, which makes the code more readable and concise. Additionally, linalg.inv() is suitable for small matrices, where the inversion process is relatively efficient and accurate.
However, linalg.inv() is not ideal for large matrices due to its computational complexity and potential numerical errors. Inverting large matrices can be computationally expensive and may consume a lot of memory. Moreover, large matrices with high condition numbers may produce inaccurate results when using linalg.inv().
Pros and Cons of linalg.solve()
The main advantage of linalg.solve() over linalg.inv() is that it is more suitable for solving linear systems of equations, which is an essential operation in many fields like engineering, physics, and finance. The solve() function is generally more accurate and faster than linalg.inv() when dealing with larger matrices.
However, linalg.solve() is not ideal for obtaining the inverse of a matrix, as it requires solving multiple linear systems of equations, which can be computationally expensive. Additionally, the function may be less intuitive to use and understand than linalg.inv().
When to Use Which Function?
In general, linalg.inv() is more suitable for small matrices with low condition numbers, while linalg.solve() is preferable for larger matrices and linear systems of equations. When using linalg.inv(), it is crucial to test the accuracy of the result by comparing it to the identity matrix or computing the condition number. On the other hand, with linalg.solve(), it is essential to check whether the solution satisfies the original equation and whether the system is solvable.
Conclusion
In conclusion, both linalg.inv() and linalg.solve() are essential functions for matrix operations in NumPy. The choice between the two depends on the specific problem and the size and condition of the matrix. It is crucial to test the accuracy of the result and be aware of the potential numerical errors that can arise when dealing with large and ill-conditioned matrices.
Thank you for taking the time to read about the differences between Numpy.Linalg.Solve() and Numpy.Linalg.Inv(). Both functions can be used for solving linear systems by inverting matrices, but the precision of their results differs.
Numpy.Linalg.Solve() is more precise when it comes to solving linear systems since it uses a more stable approach. This function uses LU decomposition to decompose matrices into lower and upper triangular matrices, which lead to more accurate solutions. Moreover, the code behind this function is optimized for both speed and reliability, making it one of the best options for solving linear systems at scale.
On the other hand, Numpy.Linalg.Inv() is less precise compared to Numpy.Linalg.Solve(). This function computes the inverse of a matrix directly, which is more straightforward but less exact when it comes to solving linear systems. Moreover, Numpy.Linalg.Inv() is prone to numerical instability, especially for large matrices.
In conclusion, choosing between Numpy.Linalg.Solve() or Numpy.Linalg.Inv() depends on the accuracy required for your particular use case. If you need high-precision results, Numpy.Linalg.Solve() is your best option. However, if you aim for reduced computational cost with moderate accuracy, Numpy.Linalg.Inv() might work just fine.
People also ask about Numpy.Linalg.Solve() vs. Numpy.Linalg.Inv(): The Precision of Matrix Inversions.
- What is Numpy.Linalg.Solve()?
- What is Numpy.Linalg.Inv()?
- What is the difference between Numpy.Linalg.Solve() and Numpy.Linalg.Inv()?
- Which function should I use for higher precision?
- What is the precision of matrix inversions in NumPy?
Numpy.Linalg.Solve() is a function in the NumPy library that solves a linear equation system. It takes two arguments, a matrix and a vector, and returns the solution to the equation system.
Numpy.Linalg.Inv() is a function in the NumPy library that calculates the inverse of a matrix. It takes one argument, a square matrix, and returns the inverse of the matrix.
The main difference between Numpy.Linalg.Solve() and Numpy.Linalg.Inv() is that Numpy.Linalg.Solve() is used to solve a linear equation system, while Numpy.Linalg.Inv() is used to calculate the inverse of a matrix.
If you need higher precision, it is generally better to use Numpy.Linalg.Solve() instead of Numpy.Linalg.Inv(). This is because Numpy.Linalg.Solve() uses an algorithm that is more accurate than Numpy.Linalg.Inv().
The precision of matrix inversions in NumPy depends on several factors, including the size of the matrix, the condition number of the matrix, and the numerical stability of the algorithm used to calculate the inverse. In general, larger matrices and matrices with a high condition number are more difficult to invert accurately.