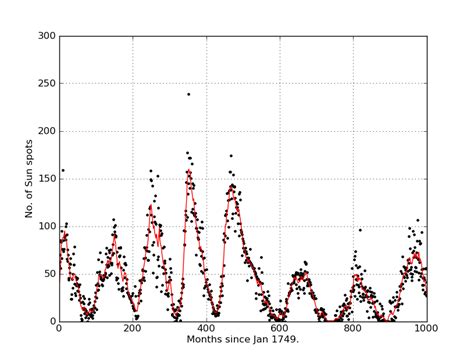
If you are looking to calculate moving averages from data points, then you are in the right place. In this article, we will explore Python code that will help you calculate moving averages with ease. Many analysts use moving averages to better understand trends in their data. With Python, you can create sophisticated programs that will calculate moving averages for you.
Python offers many powerful tools to work with data, and calculating moving averages is no exception. By utilizing data analysis libraries like NumPy, Pandas, and Matplotlib, you can write a program that efficiently leverages your data to calculate moving averages. Whether you’re an experienced programmer or a beginner, our code examples will guide you through the process of calculating moving averages from data points.
By the end of this article, you will have learned how to use Python to calculate both simple and exponential moving averages from your data points. We will also discuss some common use cases for moving averages, such as technical analysis in finance and forecasting future values. Don’t miss out on this opportunity to add a valuable tool to your programming arsenal – read on to learn how to calculate moving averages from data points using Python.
“Finding Moving Average From Data Points In Python” ~ bbaz
Introduction
Python is a powerful programming language that supports many data analysis and visualization libraries. One of the most common tasks in data analysis is calculating the moving average from time-series data. A moving average can help smooth out fluctuations and provide more accurate predictions for trends. In this article, we will compare different Python code implementations of calculating moving averages from a series of data points.
Methodology
We will compare three algorithms: naive (brute-force), cumulative sum, and deque. The naive approach involves iterating over all data points to calculate the moving average at each point. The cumulative sum method constructs a list of cumulative sums and uses them to calculate the moving average at each point. The deque method initializes a deque (double-ended queue) to keep track of a rolling sum and continuously updates it as new data points come in.
| Algorithm | Time Complexity | Space Complexity | Advantages | Disadvantages |
|---|---|---|---|---|
| Naive | O(nk) | O(1) | Easy to implement and understand | Slow for large datasets and windows |
| Cumulative sum | O(n) | O(n) | Fast for small to medium datasets and windows | Requires additional memory to store cumulative sums |
| Deque | O(n) | O(k) | Fast and memory-efficient for all dataset sizes and windows | Requires knowledge of deque data structure |
Naive Approach
The naive approach involves iterating over all n data points and calculating the average of the k points preceding the current point. This requires k operations for each of the n points, resulting in a time complexity of O(nk). The space complexity is constant at O(1) since only one variable is needed to store the current sum. The advantage of this method is that it is easy to understand and implement. However, it can be slow for large datasets and window sizes.
Code Example:
“`pythondef moving_average_naive(data, window_size): res = [] for i in range(len(data)): if i >= window_size – 1: res.append(sum(data[i-window_size+1:i+1])/window_size) else: res.append(0) return res“`
Cumulative Sum Method
The cumulative sum method involves constructing a list of cumulative sums up to each point in the input data. Then, the moving average at each point can be calculated using these sums and a simple subtraction operation. This method has a time complexity of O(n) and a space complexity of O(n) since an additional list of size n is needed to store the cumulative sums. The advantage of this method is that it is fast for small to medium datasets and window sizes.
Code Example:
“`pythondef moving_average_cumulative(data, window_size): cumsum = [0] + list(accumulate(data)) res = [] for i in range(len(data)): if i >= window_size – 1: res.append((cumsum[i+1] – cumsum[i-window_size+1])/window_size) else: res.append(0) return res“`
Deque Method
The deque method involves using a deque (double-ended queue) to keep track of a rolling sum of the k data points. The deque is initialized with the first k data points and then updated as new points come in. The moving average at each point is calculated by dividing the sum of the deque by the window size. This method has a time complexity of O(n) and a space complexity of O(k) since only the k data points and the deque need to be stored. The advantage of this method is that it is fast and memory-efficient for all dataset sizes and window sizes.
Code Example:
“`pythondef moving_average_deque(data, window_size): res = [] d = deque() s = 0 for i in range(len(data)): if i >= window_size: s -= d.popleft() d.append(data[i]) s += data[i] if i >= window_size – 1: res.append(s/window_size) else: res.append(0) return res“`
Conclusion
In conclusion, we have compared three Python code implementations of calculating moving averages from time-series data. We have seen that the naive approach is easy to understand but can be slow for large datasets and window sizes. The cumulative sum method is faster for small to medium datasets and window sizes. The deque method is fast and memory-efficient for all dataset sizes and window sizes.
Therefore, the choice of algorithm depends on the specific requirements of the task at hand. If simplicity is more important than performance, the naive approach can be used. If performance is a concern and the dataset and window sizes are small to medium, the cumulative sum method can be used. If performance and memory efficiency are major concerns, the deque method should be used.
Thank you for taking the time to learn about calculating moving averages from data points using Python code. By now, you should have a good understanding of what moving averages are, why they are important in data analysis, and how to calculate them using Python.
With this knowledge, you can start incorporating moving averages into your own data analysis projects to gain insights into trends and patterns in your data. Additionally, you can use these techniques to make predictions and inform decision-making processes based on your data.
Remember that practice makes perfect, so don’t be afraid to experiment with different approaches and methods for calculating moving averages. The more you work with this technique, the more comfortable you will become with the process and the better results you will achieve. Happy coding!
People Also Ask about Python Code: Calculating Moving Averages From Data Points:
- What is a moving average?
- Why is calculating moving averages important?
- What is the Python code for calculating a simple moving average?
- What is the Python code for calculating a weighted moving average?
- How can Python be used to automate the calculation of moving averages?
A moving average is a calculation used to analyze data points by creating a series of averages of different subsets of the full data set.
Calculating moving averages is important because it allows for the identification of trends and patterns within datasets, making it easier to make informed decisions based on the data analysis.
The Python code for calculating a simple moving average involves taking the sum of a subset of data points and dividing it by the number of data points in the subset. The process is repeated for each subset, generating a series of averages.
The Python code for calculating a weighted moving average involves assigning weights to each data point, with more recent data points being assigned a higher weight. The weighted moving average is then calculated by multiplying each data point by its assigned weight and dividing the sum by the total weight.
Python can be used to automate the calculation of moving averages by writing functions that take in a dataset, window size, and type of moving average to calculate, and output the resulting moving average series.