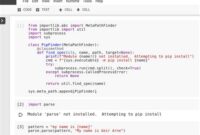
Are you curious about the different techniques for representing graphs in Python? Look no further, as this comprehensive guide will take you through all the different methods and give you a complete understanding of each one.
Whether you’re a beginner or already familiar with programming, this guide has something for everyone. Not only will you learn ways to represent graphs using built-in data structures, but you’ll also discover external packages that can simplify the process even further.
From dictionaries to adjacency matrices, this article covers it all. You’ll also gain knowledge of how to implement algorithms like Dijkstra’s shortest path algorithm using these representations.
Whether you’re a student learning about graph theory or a developer trying to solve real-world problems, this guide on Python techniques for representing graphs is a must-read. So dive in and unravel the mystery of graph representation in Python with ease.
“Representing Graphs (Data Structure) In Python” ~ bbaz
Introduction
When it comes to representing graphs in software development, Python offers a wide range of techniques. However, each technique has its advantages and disadvantages, making it crucial for developers to pick the best method that suits their specific use case. This blog article will delve into the most prominent Python techniques for representing graphs and compare them side by side.
Adjacency Matrix
Description
An adjacency matrix is a square matrix that represents the connections between nodes (vertices) in a graph. The matrix contains a binary value that indicates whether there is an edge between a pair of vertices.
Advantages
- Easy to implement and visualize
- Faster access to connectivity data
- Works well with small graphs
Disadvantages
- Memory-intensive for large graphs
- Adding or removing vertices requires resizing the entire matrix
Adjacency List
Description
An adjacency list is a collection of lists that represents the connections between vertices. Each vertex is associated with a list of its neighbours.
Advantages
- Memory-efficient for large graphs
- Adds vertices without rescaling the whole structure
- Flexible for varying edge weights
Disadvantages
- Slow retrieval of connectivity information
- Time-consuming to search for a specific edge
Edge List
Description
An edge list is a collection of pairs that represent the edges in a graph. Each pair contains the vertices that are connected by an edge.
Advantages
- Memory-efficient for sparse graphs
- Easy to create and manipulate
- Flexible for varying edge weights
Disadvantages
- Slow retrieval of vertex neighbour information
- Not optimal for dense graphs
Comparison Table
| Technique | Advantages | Disadvantages |
|---|---|---|
| Adjacency Matrix | Easy implementation, faster access, good for small graphs | Memory-intensive for large graphs, slow resizing |
| Adjacency List | Memory-efficient, flexible for varying edge weights, easy scalability | Slow retrieval of connectivity data, slow searching for a specific edge |
| Edge List | Memory-efficient for sparse graphs, easy manipulation | Slow retrieval of neighbouring vertices, not optimal for dense graphs |
Conclusion
Each technique has its advantages and disadvantages, so it is important to consider the specific use case when selecting the most suitable approach. For small graphs, the adjacency matrix may be a good option, while larger or denser graphs may benefit from using an adjacency list or edge list. The edge list may be perfect for sparse graphs. Regardless of the choice, Python offers a range of techniques that can represent graphs efficiently with the right implementation.
Python Techniques for Representing Graphs: A Comprehensive Guide
Thank you for taking the time to explore this comprehensive guide on Python techniques for representing graphs. As you have read, graphs are a powerful tool for analyzing complex data relationships and allowing for efficient problem solving.
In this guide, we’ve discussed various graph representation techniques, including adjacency lists, adjacency matrices, and edge lists. Each of these techniques has its own strengths and weaknesses, and it’s important to understand when and how to use them effectively in your work.
We hope that this guide has provided you with a solid foundation for working with graphs in Python. However, it’s just the beginning! There’s still much more to learn, such as advanced algorithms for graph traversal and pathfinding. We encourage you to continue exploring and experimenting with graphs to unlock their full potential!
Once again, thank you for reading. We wish you all the best in your Python programming journey!
Python Techniques for Representing Graphs: A Comprehensive Guide is a must-read for anyone interested in graph theory and its implementation in Python. Here are some of the most commonly asked questions about this topic:
1. What are the different ways to represent a graph in Python?
There are several ways to represent a graph in Python, including:
- Adjacency Matrix
- Adjacency List
- Edge List
- Incidence Matrix
2. How do I implement Dijkstra’s algorithm in Python?
Dijkstra’s algorithm is a popular graph traversal algorithm used to find the shortest path between two nodes in a weighted graph. Here’s an implementation in Python:
- Create a dictionary of vertices and their distances from the starting node.
- Create a set of unvisited vertices.
- While the set of unvisited vertices is not empty:
- Find the vertex with the smallest distance from the starting node.
- Mark that vertex as visited.
- For each neighbor of the current vertex:
- If the distance to the neighbor through the current vertex is less than its current distance, update it.
3. What is a spanning tree?
A spanning tree is a subgraph of a graph that includes all of its vertices but only a subset of its edges. It must be a tree (i.e., acyclic and connected).
4. How can I implement Kruskal’s algorithm in Python?
Kruskal’s algorithm is a popular minimum spanning tree algorithm. Here’s an implementation in Python:
- Sort the edges of the graph by weight.
- Create a set for each vertex.
- For each edge in the sorted list:
- If the vertices of the edge are in different sets, add it to the minimum spanning tree and merge the sets.
5. What is a directed acyclic graph?
A directed acyclic graph (DAG) is a directed graph with no cycles. It is often used to represent dependencies between tasks or events.