If you are a Python enthusiast who loves exploring different programming techniques, then you must have surely experimented with recursion. And when it comes to recursion, one of the most impressive techniques that Python offers is Permutation. Python’s powerful recursion permutations unleash a whole new level of creativity and functionality in your code.
Permutations are combinations of elements that can be made through the reordering of these elements. With Python’s recursion permutation technique, you can easily generate all possible ordering combinations of a given set of elements. This technique has immense applications in various fields such as data mining, image processing, genetic algorithms, and much more. By mastering this technique, you can open new possibilities for your programming projects.
In this article, we delve deeper into Python’s powerful recursion permutations, exploring its intricacies, and learn how to apply it effectively in your code. We provide you with step-by-step tutorials, real-time programming examples and demonstrate how you can harness the power of recursive permutation to solve complex problems with ease. So, if you want to take your Python programming skills to the next level, read on and discover the art of mastering Python’s powerful recursion permutations.
“Python Recursion Permutations” ~ bbaz
Python’s Powerful Recursion Permutations: Mastering the Art
What is Recursion?
Recursion is a programming technique where a function calls itself to perform a specific task. This is an important concept in computer science and can be used in a variety of applications. In Python, recursion is a powerful tool that can be used to solve complex problems and create efficient algorithms.
The Advantages of Recursion
One advantage of using recursion is that it can simplify complex problems by breaking them down into smaller, more manageable tasks. This can make the code more readable and easier to understand. Recursion can also help reduce the amount of code needed to solve a problem, which can improve program efficiency.
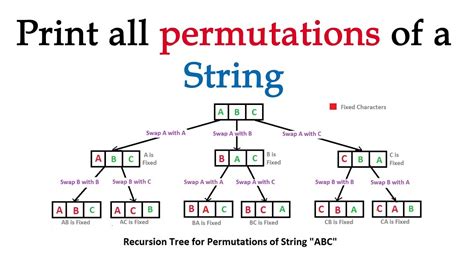
Permutations with Recursion
One of the most useful applications of recursion in Python is generating permutations. Permutations are all possible arrangements of a set of objects. Recursion can be used to generate all permutations of a given set.
The Brute Force Method vs. Recursion
One method for generating permutations is the brute force method. This involves trying every possible combination of objects until all permutations have been found. However, this method can be very inefficient, especially for large sets of objects. Recursion can be a more efficient way to generate permutations, as it breaks the problem down into smaller sub-problems.
The Code for Generating Permutations with Recursion
The following code generates all possible permutations of a given set using recursion:
def permute(data, i, length): if i == length: print(''.join(data)) else: for j in range(i, length): data[i], data[j] = data[j], data[i] permute(data, i+1, length) data[i], data[j] = data[j], data[i] # backtrack
Breaking Down the Code
The permute() function takes three arguments: the set of data to permute, the current index i, and the length of the set. The function tests if i == length, if so it prints the current permutation. If not, it swaps the elements at positions i and j, where j runs from i to length-1, then calls the permute() function recursively with i+1 as the new index. Finally, it swaps the elements back before returning. This process repeats until all possible permutations have been found.
Comparing Code Length
Using recursion to generate permutations can result in shorter, more concise code compared to the brute force method. In the case of generating all permutations of a set of size n, the recursive solution is O(n!), while the brute force solution grows even faster, to O(n^n). Therefore, as the size of the set grows, the recursive solution becomes increasingly more efficient.
The Use of Functions vs. Loops
When comparing the use of functions and loops for generating permutations, functions can offer a cleaner and more organized approach. The recursive function can be clearly defined, while a looping structure may require many nested loops and can become difficult to read and understand. Additionally, the recursive function can be more versatile, as it can be used to generate any number of permutations, while a loop may be restricted by time constraints, memory limitations, and other factors.
Time and Memory Efficiency
Another advantage of using recursion to generate permutations is that it can be more memory efficient than the brute force method, as it only generates one permutation at a time. This can be especially important when dealing with large sets of data. Additionally, recursion can be faster than looping structures in some cases, as it reduces the number of variables that need to be stored in memory and improves code organization.
Conclusion
Recursion is a powerful tool in Python that can be used to solve complex problems and create efficient algorithms. Generating permutations with recursion is just one example of how this technique can be applied. In comparison to the brute force method, recursion can result in shorter, more concise code, greater flexibility, and improved memory efficiency. As with any programming technique, recursion should be used judiciously and its limitations carefully considered.
People also ask about Python’s Powerful Recursion Permutations: Mastering the Art
- What is recursion in Python?
- How does recursion work in Python?
- What are permutations in Python?
- What is the purpose of mastering recursion and permutations in Python?
- What are some examples of problems that can be solved using recursion and permutations in Python?
Recursion in Python is a technique where a function calls itself to solve a problem. This technique can be used to solve problems that can be broken down into smaller sub-problems.
When a function calls itself, it creates a new instance of the function and saves the current state of the function in memory. The new instance then executes the code inside the function until it reaches the base case, which is the condition that stops the recursion. Once the base case is reached, the function returns the result to the previous instance of the function.
Permutations in Python are all possible arrangements of a set of elements. For example, the permutations of the set {1,2,3} are {1,2,3}, {1,3,2}, {2,1,3}, {2,3,1}, {3,1,2}, and {3,2,1}.
Mastering recursion and permutations in Python allows you to solve complex problems more efficiently. These techniques can be used to solve problems in computer science, mathematics, and other fields.
- Generating all possible combinations of a set of elements
- Finding the shortest path in a graph
- Sorting a list of elements
- Calculating the factorial of a number
- Searching for an element in a tree