Solving Orbiting Body Position with RK4 in Python: Troubleshooting

Are you struggling with calculating the position of orbiting bodies using RK4 in Python? Are you tired of constantly encountering troubleshooting issues? Look no further! This article will guide you through the process of solving orbiting body position using RK4 and provide tips for troubleshooting any errors you may encounter along the way.

RK4, or the fourth-order Runge-Kutta method, is a popular numerical technique used for solving differential equations. In this case, we are using it to calculate the position of orbiting bodies, such as planets or satellites, in space. However, implementing RK4 in Python can be tricky and requires a solid understanding of both the method and the programming language itself.

This article will cover the basic steps of using RK4 to solve orbiting body position in Python, including how to set up your initial conditions, define your differential equation, and iterate through each step of the calculation. It will also provide troubleshooting tips for common errors that may arise, such as incorrect syntax or incorrect integration time steps.

By the end of this article, you will have a clear understanding of how to solve orbiting body position using RK4 in Python and be fully equipped to tackle any troubleshooting issues that may come your way. So, whether you’re a beginner programmer or an experienced mathematician, read on and discover the ways of mastering RK4 in Python!

“Cannot Get Rk4 To Solve For Position Of Orbiting Body In Python” ~ bbaz

Introduction

Orbiting body position is a fundamental concept in celestial mechanics. It is essential for space exploration and satellite systems. Solving orbiting body position is a complex problem that requires advanced mathematical techniques. In this article, we will discuss how to solve orbiting body position with RK4 in Python and its troubleshooting techniques.

What is RK4?

RK4 is a fourth-order numerical integration method that is widely used to solve ordinary differential equations. It is a popular method due to its simplicity and accuracy. RK4 is an iterative method that uses the current state of a system to estimate the next state. It provides a more accurate solution compared to other numerical methods such as Euler’s method.

Solving Orbiting Body Position with RK4

The position of a satellite or a celestial object can be defined in terms of its x, y, and z coordinates. The motion of the object can be described by a system of differential equations. These differential equations can be solved numerically using RK4. The steps involved in solving orbiting body position with RK4 are:

1. Define the initial conditions, i.e., the initial positions, velocities, and accelerations of the object.
2. Write the equations of motion for the object in terms of its x, y, and z coordinates.
3. Use RK4 to solve the system of equations iteratively over a specified time period.
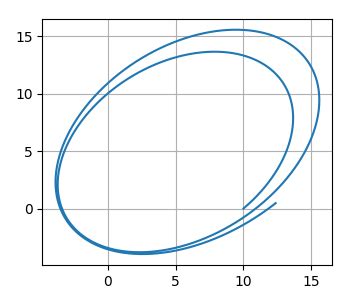
4. Plot the position of the object at each time step to visualize its orbit.

Sample Code in Python

Here is a sample code in Python that uses RK4 to solve orbiting body position:

def rk4(f, t0, y0, h, tf): k1 = f(t0, y0) k2 = f(t0 + h / 2, y0 + (h / 2) * k1) k3 = f(t0 + h / 2, y0 + (h / 2) * k2) k4 = f(t0 + h, y0 + h * k3) y1 = y0 + (h / 6) * (k1 + 2 * k2 + 2 * k3 + k4) if t0 + h >= tf: return y1 else: return rk4(f, t0 + h, y1, h, tf)

Troubleshooting

Solving orbiting body position with RK4 can encounter several issues. Some of the common problems include:

Accuracy Issues:

RK4 is a numerical method that can introduce errors in the solution. The accuracy of the solution depends on the step size used in the iteration process. If the step size is too large, the solution may be inaccurate. To ensure the accuracy of the solution, it is essential to use a small enough step size while iterating.

Convergence Issues:

There are cases when RK4 fails to converge to a solution. This can happen if the differential equations have singularities, e.g., division by zero. In such cases, we need to modify the equations or use a different numerical method to solve the problem.

Computational Complexity:

The RK4 method requires multiple iterations to solve the system of equations. As the number of iterations increases, the computational complexity increases. This can lead to longer execution times, especially for large-scale problems.

Comparison with Other Methods

RK4 is one of the most popular numerical methods used to solve differential equations. However, other numerical methods can also be used to solve orbiting body position. Some of the commonly used methods include:

1. Euler’s Method: It is a simple and straightforward method that iteratively approximates the solution of differential equations. However, it has lower accuracy than RK4, leading to less accurate solutions.
2. Leapfrog Method: This method uses a staggered time-grid to calculate the solution. It is more accurate than Euler’s method but less accurate than RK4.
3. Verlet Method: This method is used to solve Lagrangian equations of motion. It is highly accurate and provides symmetric solutions, making it suitable for many physical problems.

Conclusion

In conclusion, solving orbiting body position with RK4 in Python is an essential tool for space exploration and satellite systems. RK4 provides an accurate and reliable solution for complex problems. However, it is not immune to issues such as accuracy, convergence, and computational complexity. It is necessary to understand these issues and devises troubleshooting techniques to solve them. Overall, RK4 is a powerful tool that has contributed significantly to the advancement of human space exploration.

Thank you for taking the time to read our article about solving orbiting body position with RK4 in Python. We hope you found the information informative and valuable as you work to troubleshoot your own code.

If you have any questions or further concerns, please feel free to leave a comment below or contact us directly. We are always happy to help fellow programmers and problem-solvers overcome obstacles and achieve success in their projects.

Remember, persistence and patience is key when it comes to coding. Don’t be discouraged if it takes several attempts to get your program running smoothly. With perseverance and the use of techniques like RK4, you can solve even the most complex programming challenges.

Here are some common questions or concerns that people may have when trying to solve orbiting body position with RK4 in Python:

1. Why am I getting inaccurate results?

   One possible reason for inaccurate results is that your step size is too large. Try reducing the step size and see if that improves the accuracy. Another possibility is that there is an error in your implementation of the RK4 algorithm. Check your code for any mistakes or typos.

2. How can I plot the orbit?

   You can use Matplotlib to create a 3D plot of the orbit. First, you will need to store the position data in arrays. Then, you can pass those arrays to Matplotlib’s plot_surface function to create a 3D plot.

3. What units should I use?

   The units you use will depend on the specific problem you are trying to solve. However, it is important to be consistent with your units throughout your calculations. Some common units used in orbital mechanics include meters, kilograms, and seconds.

4. How can I add more bodies to the simulation?

   To add more bodies to the simulation, you will need to modify your equations of motion to take into account the gravitational forces between all the bodies. You will also need to store the position and velocity data for each body in separate arrays. Finally, you can plot the orbits of all the bodies using Matplotlib.

5. Can I use RK4 for other types of problems?

   Yes, RK4 can be used to solve a variety of differential equations, not just those related to orbital mechanics. However, the specific implementation of RK4 may vary depending on the problem being solved.